Reubicación de instalaciones productivas mediante método matemático de recálculo de coordenadas MMRC

INTRODUCCIÓN

Es notable cómo, a través de la historia, los mercados de bienes y servicios han venido evolucionando e incrementando sus niveles de producción en las esferas locales, nacionales e internacionales, alcanzando, incluso, a duplicarse. Así mismo, se ha incrementado el consumo y, con ello, las exigencias de calidad que deben poseer estos productos: resulta vehemente el cumplimiento de sus requerimientos (Organización Mundial del Comercio – OMC, 2016, p.11). Por lo tanto, las organizaciones de toda índole alrededor del mundo se ven en la obligación de seguir el ritmo de la evolución del mercado y de cumplir con sus requerimientos, a fin de no terminar por fuera de este, dado que deben optimizar sus operaciones y generar un valor agregado al cliente. 

Al respecto, autores como Chen (2001), Jafarian, Azizolah, Mehdi y Seyed (2009) y Demirel, Demirel y Cengiz (2010), argumentan que la consolidación y centralización de la producción en un emplazamiento productivo es una excelente iniciativa para la reducción de los costos de inversión, el incremento en la calidad del producto ofrecido, la visibilidad y la oferta continua del producto, el aprovechamiento de economías de escala y el cumplimiento de los objetivos de la cadena de suministros, en sus bajos costos y en su alta capacidad de respuesta.

Por estos motivos, la ubicación de un emplazamiento productivo se ha convertido en uno de los problemas de decisión más importantes para la distribución de bienes de forma eficiente por parte de una organización (Chen, 2001; Huang, Menezes y Kim, 2012; Causado y Reatiga, 2013). Al respecto, se aclara que existen muchos métodos para dar solución al problema de localización de emplazamientos productivos, pero en el caso de un solo emplazamiento o centro de acopio, como es el interés de este estudio, se concretan diversas técnicas, tales como: el método de centro de gravedad o el método de Weber, el método de la cuadricula, el método del centroide, el modelo de Brown y Gibson, el método de preferencias jerárquicas, el método de factores ponderados, entre otros (Ballou, 2004; Arsanjani, Helbich, Kainz y Bolooranic, 2013; Urango, Pérez y Romo, 2015).

En este contexto, para llevar a cabo la ubicación de emplazamientos productivos en el presente estudio se procederá de manera secuencial, mediante la aplicación del Método de Centro de Gravedad, de carácter netamente cuantitativo, en combinación posterior con el Método Matemático de Recálculo de Coordenadas – MMRC, de carácter inédito, el cual concreta ciertos factores cualitativos; esto, debido a que el caso del primer método se basa en la idea de que interesa minimizar los costos de transporte totales, a fin de hallar el punto en el que la suma de los costes de transporte a todos los puntos de origen y destino sea mínima (Weber, 1922) o, en palabras más explicitas de Ares (2003), cuanta más demanda congregue un punto es mucho más interesante ubicarse cerca de él, pues “cada punto de demanda o producción atrae al almacén hacia sí, con una fuerza directamente proporcional al producto del coste unitario de transporte y al flujo de materiales que sale o llega a ese punto”(p, 51). 

En cuanto al Método Matemático de Recálculo de Coordenadas – MMRC, con respecto al sector agrícola, por ser productos perecederos los manejados allí, estos han de llegar al centro de acopio y ser redistribuidos de forma inmediata (en la medida de lo posible) con cierto valor agregado, mediante operaciones de Cross Docking, de forma que se establezcan supuestos de la realización de cargas completas para ser transportadas a los centros de demanda estipulados, siendo habitual, en la aplicación de estos métodos, la minimización de los costos de transporte (Turkesteen y Klose, 2012). En este sentido, resulta de interés y se justifica el uso del método de centro de gravedad dado que representa un análisis sencillo del problema, ya que estipula que la demanda y su ubicación son conocidas, tal cual, a los casos aplicados en el presente ejercicio.

Sin embargo, aun cuando se encuentre la ubicación del emplazamiento con la aplicación de uno de los métodos anteriores, la tarea no termina ahí: con el método de ubicación aplicado en este caso (Centro de Gravedad), solamente se hace un análisis de los factores de demanda y de las coordenadas de estos puntos de demanda, a fin de ubicar el emplazamiento productivo sin tener en cuenta que dicha ubicación puede estar susceptible a factores que no pueden ser controlables, tales como los de carácter social, económico, ambiental, político, entre otros (Melkote y Daskin, 2001; Sánchez, 2007; Albornoz y Johns, 2011; González, 2014).

En este ámbito, autores como Laporte (1992), Garrocho (2003), Ballou (2004), Chase, Jacobs y Aquilano (2009) adaptaron formalmente este tema, en el marco de la gestión de cadenas de suministros y de la investigación de operaciones, mediante formulación de modelos matemáticos para solución de problemas de transporte y distribución de manera óptima. Por lo tanto, el presente escrito plantea la aplicación de uno de estos métodos para lograr la ubicación del emplazamiento productivo y el posterior ajuste de este, con un nuevo método diseñado por los autores presentes, en el caso en que esta ubicación no resulte adecuada, debido a que pueden terminar, según sus coordenadas, en la mitad de una vía, en plena zona escolar o, quizá, en un área protegida o de conservación.

Dentro de este contexto, la localización puede verse influenciada por aspectos como costos, impuestos, salarios, rentas, vías, materias primas, entre otros (Guan, Li, Inahoe, Su, Nagaie y Hokao, 2011). Así mismo, Sun, Forsythe y Waters (2007) y Causado, García, Martínez y Herrera (2015) indican la necesidad de evaluar los determinantes que se puedan llegar a descartar en el escenario del incumplimiento de, por lo menos, una de las dos condiciones siguientes: 1) El factor tiene que ser sensible a la localización; es decir, no se tomarán en cuenta aquellos factores que no sean afectados por las decisiones sobre localización. 2) El factor debe tener un fuerte impacto en la capacidad de la empresa para alcanzar sus metas. Por su parte, Behera, Borate, Panda, Behera y Roy (2012) manifiestan que las alternativas de localización incluyen:

1. Expandir una instalación existente en lugar de moverla. 2) Mantener los sitios actuales mientras se abren instalaciones en algún otro lugar. 3) Cerrar las instalaciones existentes y cambiarse a una nueva localización. De acuerdo a esto, tomar la decisión de una localización es un proceso que, generalmente, es trascendental, puesto que este puede incidir, incluso, tanto en el éxito como el fracaso de toda la organización (p. 1012).

Por el contrario, autores como Posada (2011) y Feldmann y Olhager (2013) proponen la necesidad de realizar el análisis de la localización del empleo manufacturero y de los servicios superiores mediante el uso de cocientes de localización; esto, a fin de atender los criterios fundamentales de la región de pertenencia y el tamaño urbano, investigando el rol estratégico de las plantas, en términos del tipo y nivel de competencia del sitio, su relación con la razón estratégica de la ubicación y el impacto en el desempeño operativo. Sobre este mismo tema, Sánchez (2007) y González (2014) determinaron, en su estudio acerca de los condicionantes para la facilidad y sostenibilidad de instalaciones de manufactura, que la aglomeración geográfica de poder político, la influencia económica y la articulación internacional son factores esenciales que pueden revelar las decisiones de ubicación de un emplazamiento productivo.

No obstante, de manera generalizada las organizaciones tienen limitaciones respecto a la nueva ubicación de sus emplazamientos: entre estas, limitaciones económicas, aspectos ambientales o sociales. Un método como el de centro de gravedad permite encontrar geométricamente el punto ideal que presenta el mayor beneficio para la empresa, pero es probable que esa ubicación calculada ya se encuentre ocupada o no sea viable por alguna de las restricciones a la actividad productiva desarrollada (Garrido y San Martín, 2015). Actualmente, si se presenta esa situación, la forma de reubicar las coordenadas es simplemente moverlas arbitrariamente hasta donde sean viables y menos alejadas de la ubicación ideal inicial. Afortunadamente, mediante el MMRC planteado en este escrito se ofrece una alternativa viable, eficaz y con menor subjetividad para la reubicación de emplazamientos productivos a través del recálculo de coordenadas.

En este ámbito, el presente artículo busca responder a las preguntas: ¿Por qué es importante la ubicación de emplazamientos productivos mediante el recálculo de coordenadas? ¿Cuán factible es recalcular coordenadas para la reubicación de emplazamientos productivos? Y, finalmente, la pregunta más importante a resolver por el estudio es: ¿De qué manera el nuevo Método Matemático de Recálculo de Coordenadas – MMRC aporta en la definición final de emplazamientos productivos?

El presente artículo se desarrolló de la siguiente manera: una primera sección con introducción, contexto y articulación de aspectos teóricos relacionados a la temática con el entorno; una segunda sección, con un proceso metodológico, en la cual se presenta de forma detallada el proceso de aplicación de los métodos de centro de gravedad y el nuevo Método Matemático de Recálculo de Coordenadas – MMRC; una tercera sección, de presentación de resultados del levantamiento, selección, clasificación y evaluación de la información; una cuarta sección, en la que se presenta una discusión y conclusiones, y, por último, las respectivas referencias bibliográficas.

METODOLOGÍA

Con el ánimo de constatar la aplicación de herramientas y técnicas de la Ingeniería Industrial a procesos de definición de sitios, que permitan la ubicación de emplazamientos productivos, se presenta, de manera detallada, la aplicación de los métodos de ubicación de emplazamientos productivos (Método de Centro de Gravedad y el nuevo Método Matemático de Recálculo de Coordenadas MMRC), a fin de evaluar, de manera concreta, las coordenadas que faciliten la ubicación del centro de agregación productiva de interés de manera correspondiente.

Método de Centro de Gravedad

Heizer y Render (2004) manifiestan que “el método del centro de gravedad es una técnica matemática que se usa para encontrar la localización de un centro de distribución que minimice los costos de distribución” (p. 309). A su vez, este método de localización permite su fácil aplicación puesto que el origen del sistema coordenado y la escala usada son arbitrarios, siempre y cuando las distancias relativas se representen de manera correcta para su implementación, teniendo en consideración las instalaciones que ya existen, las capacidades de producción y volúmenes, la ubicación y distancias entre ellas; esto, bajo el supuesto de que los costos de transporte de entrada y salida son iguales y de que no incluye costos de envío especiales por menos que cargas completas (Ballou, 2004, p.555). Una vez se tienen las localizaciones en el sistema coordenado, el centro de gravedad se determina mediante la aplicación de las ecuaciones 1 y 2 (Haizer y Render, 2004, p.309):

Donde
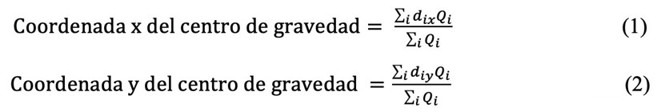
d_ix = Coordenada x de la localización i
d_{_iy} = Coordenada y de la localización i
Q_i = Cantidad de bienes que se lleva desde o hacia la localización i

Método Matemático de Recálculo de Coordenadas MMRC

De acuerdo con los autores de esta propuesta, se procede con la definición del nuevo Método Matemático de Recálculo de Coordenadas (MMRC), el cual se encuentra basado en la teoría de la localización industrial de Weber; a su vez, este método busca poder reubicar coordenadas bajo parámetros concretos que permitan fijar una ubicación alternativa determinable como la mejor después de la calculada con el método de centro de gravead. Dichos parámetros han de analizar la situación inviable y fijar qué tanto debe moverse la coordenada para garantizar el mayor beneficio, que es la ubicación real y final del establecimiento productivo del caso.

El MMRC es de carácter mixto, tanto cualitativo como cuantitativo; además, analiza y propone una nueva localización a partir de la inviabilidad alcanzada con el método de centro de gravedad, la cual pudo haber sido definida por cualquiera de los métodos pertinentes de la teoría de la localización, evaluando la problemática desde dos aspectos fundamentales: la necesidad de cambio que se tiene y el factor causante de dicho cambio (denominado “factor de inviabilidad”). Cada uno de estos aspectos se enmarca en un instrumento de medida de acuerdo a la experticia de los autores a partir de ponderaciones predeterminadas (Tabla 1).

Tabla 1.
Ponderación de necesidades de cambio y factores de inviabilidad

Fuente elaboración propia

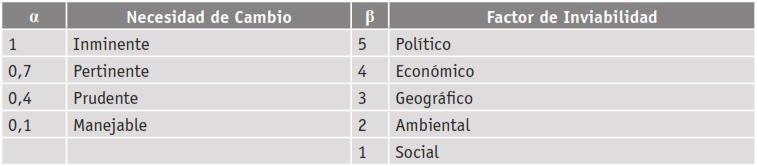
α: Necesidad de cambio: (1) Inminente: no existe ninguna forma mediante la cual se pueda adaptar la ubicación. (2) Pertinente: mediante algunos cambios es posible ubicar la instalación en las coordenadas, pero por determinado motivo (económico, medioambiental, social, etc.) se recomienda reubicar. (3) Prudente: mediante algunos cambios es posible ubicar la instalación en las coordenadas, pero no presenta garantías en el futuro. (4) Manejable: mediante algunos cambios es posible ubicar la instalación en las coordenadas. Este criterio se califica de acuerdo a la urgencia de la necesidad de cambio del sitio del emplazamiento, previo cálculo de coordenadas a través del método de centro de gravedad, tomando valores así: 1 cambio inminente; 0,7 cambio pertinente; 0,4 cambio prudente; 0,1 cambio manejable.

A su vez, α: el factor de inviabilidad: (5) Político: negación gubernamental o burocrática de cualquier índole. (4) Económico: Los costos de ubicar son muy elevados. (3) Geográfico: ya existe una estructura o espacio natural en las coordenadas y esta no puede ser reubicada. (2) Ambiental: la ubicación no es sostenible ambientalmente de ningún modo. (1) Social: la ubicación de la instalación en las coordenadas generan un daño social que no es posible asumir. El criterio jerárquico de clasificación de este factor se estableció de acuerdo a juicio de expertos en ubicación de emplazamientos productivos de la universidad del Magdalena, en el marco del proyecto de investigación “Caracterización logística agroindustrial del departamento del Magdalena”, financiado por FONCIENCIAS.

Por consiguiente, las ponderaciones y aspectos tenidos en cuenta en este caso permiten analizar varios escenarios, incluyendo uno que normalmente es ignorado como lo es el factor político, en el cual se incluye desde la negativa de uso del suelo por proyectos gubernamentales en los que se plantea dicho uso, hasta la necesidad de proyectos de conveniencia y/o de restitución de derechos vulnerados. A la hora del análisis, es importante no confundir el factor económico con los demás ya que es muy fácil que esto ocurra. Se habla de factores geográficos, ambientales y sociales cuando no es posible remediar el daño o usar la ubicación de manera integral y sostenible de ninguna forma. Este método se puede usar independientemente del tipo de estructura productiva o de servicio (pública o privada) que se vaya a reubicar; pero esto último debe estar definido junto con todos sus aspectos antes de realizar el análisis, puesto que cada caso en particular tendrá una incidencia distinta en el cálculo de los factores y viceversa.

Junto a los aspectos mencionados, para el análisis se tendrá en cuenta el número de factores que presenta el escenario (α = 1, 2, 3…), que serán tantos como se considere y la coordenada de la ubicación ideal (X ó Y). La resolución matemática presenta algunas propiedades: (1) el análisis de reubicación mantiene independencia entre los ejes plano, por lo cual se analiza cada coordenada; (2) debe existir proporcionalidad en las unidades de las coordenadas y el mapa; (3) la dirección de la nueva posición será perpendicular al factor de inviabilidad o a la suma de ellos (en donde cada una de las coordenadas se moverá en sentido contrario); (4) es aplicable una vez se haya llegado a la ubicación ideal no viable del emplazamiento por cualquier método de los explicados con anterioridad (Ec. 4, 5 y 6).

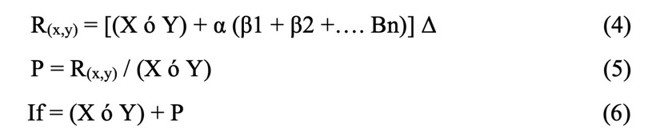
Lo que el MMRC determina es el porcentaje de una unidad de medición en que debe moverse la coordenada; por lo tanto, se define como la proporcionalidad de la coordenada según los aspectos analizados. Ri: define la relación entre los factores de inviabilidad y la necesidad de cambio (Ec. 4); P: sirve como base de comparación para determinar el índice de proporcionalidad (Ec. 5); If: se define como la nueva coordenada, relacionando la coordenada inicial con el índice de proporcionalidad, donde el signo estará definido por la dirección en el plano para donde sea conveniente mover el emplazamiento productivo (Ec. 6).

RESULTADOS

A continuación, a fin de evidenciar la respectiva aplicabilidad del nuevo método, se presentan dos casos de aplicación del MMRC.

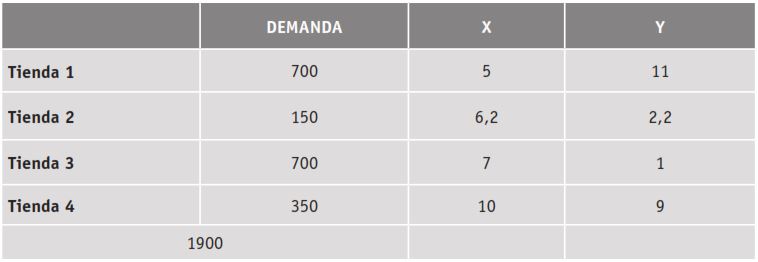
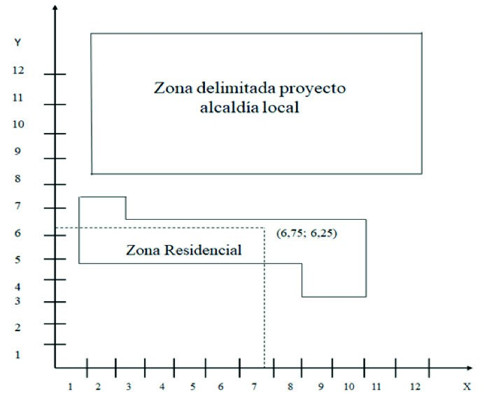
Primer caso (factor político): mediante datos de la Secretaría de Desarrollo Económico, la asociación de comercializadores de frutas en el Distrito Turístico, Cultural e Histórico (D.T.C.H) de Santa Marta – Colombia, pretende establecer un centro de acopio y un centro de distribución para sus cuatro tiendas; para esto, aplica el método de centro de gravedad a fin de determinar las coordenadas ideales, que fueron: (6,75; 6,25) (Tabla 2).

Tabla 2.
Datos de demanda y coordenadas (X, Y), de posible ubicación de emplazamientos de la asociación de comercializadores de frutas del D.T.C.H, de Santa Marta.

Fuente elaboración propia

Esta ubicación se encuentra entre una zona residencial y un proyecto ejecutado por la alcaldía local, por lo cual no es viable, presentando dificultad de acceso para vehículos pesados. En el lugar también se realizarán procesos de lavado, pelado y empaque de frutas para su distribución; dichos procesos generan material de desecho. La empresa necesita reubicar el emplazamiento a través del cálculo de las nuevas coordenadas lo más cerca posible de la posición ideal. Además, la zona residencial no se vende por ningún motivo (Figura 1).

Para este caso, se puede observar que la ubicación se encuentra en medio de dos factores de cambio: por un lado, el proyecto de la alcaldía se puede identificar como un factor político; por otro lado, para caracterizar la zona residencial es importante la negativa de venta del inmueble. A partir de allí, el “comprar” no es una solución, por lo cual no se estaría hablando de un factor económico: se está en presencia de un factor de cambio social, debido a que esta población se vería hipotéticamente afectada por la generación de desechos sólidos. Aunque se podrían asumir costos en tecnología para reducir la cantidad de desechos líquidos y sólidos generados, no hay forma de facilitar el acceso para cargue y descargue. En este escenario, las coordenadas serán movidas, atravesando uno de los factores en la dirección contraria del factor que posea la mayor relación magnitud/importancia; en este caso, el factor político. Al existir una posibilidad remota de ubicación en la posición ideal, se considera la necesidad de cambio como pertinente.

Figura 1.
Ubicación preliminar del centro de distribución.

Fuente: elaboración propia

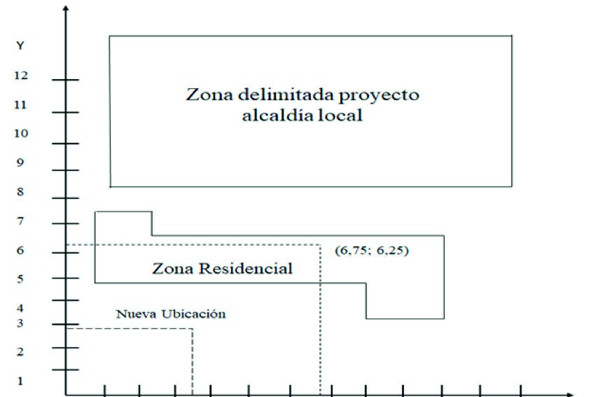
Al ser analizadas las coordenadas obtenidas (3,51; 2,91), se tiene una ubicación disponible, lo más cerca posible de la ideal y por fuera de cualquier situación conflictiva con los habitantes de estas áreas del municipio, dado que no afecta la zona residencial ni la zona del proyecto de la Alcaldía local (Figura 2).

Figura 2.
Nueva ubicación del centro de distribución.

Fuente: elaboración propia

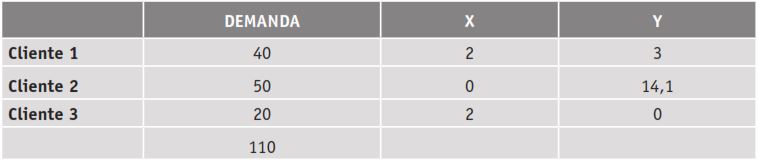
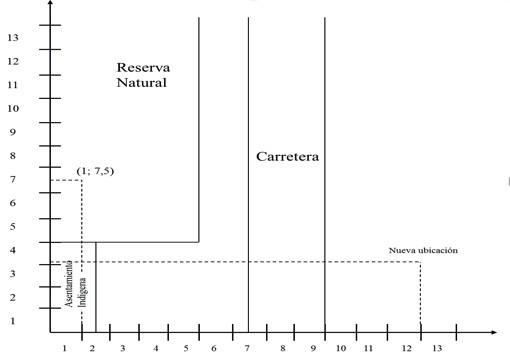
Para el segundo caso, donde se hace referencia a los factores sociales de la zona, un empresario de frutas y hortalizas del municipio de Ciénaga – Magdalena – Colombia decide crear un centro de acopio para sus productos de modo que desde allí se distribuyan a todos sus clientes, manteniendo el menor costo posible de transporte desde cada una de sus fincas. Mediante el método de centro de gravedad, se determinó que la ubicación ideal está en las coordenadas (1; 7,5) (Tabla 3).

Tabla 3.
Datos de demanda y coordenadas de posible ubicación de centro de acopio de frutas en el municipio de Ciénaga, Colombia.

Fuente: elaboración propia

Figura 3.
Ubicación ideal del centro de acopio.

Fuente: elaboración propia

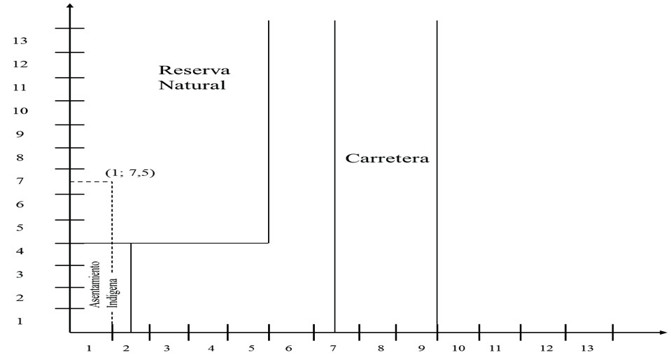
Antes de realizar el análisis de reubicación, es vital conocer toda la información del escenario planteado. Se presentan diferentes aspectos que requieren un estudio previo para la correcta aplicación del MMRC. La ubicación planteada para el centro de acopio se encuentra sobre una reserva natural, la cual colinda con un asentamiento de indígenas que suelen cazar y sembrar, así como realizar otras actividades en los alrededores de la parte oriental de esta área. Además de esto, se encuentra una carretera en la zona. Se asume que la parte de las zonas no se encuentran delimitadas, dando a entender su continuidad y gran tamaño o, por lo menos, mayor a la parte representada.

Se pueden definir la carretera y la reserva natural como un factor geográfico (siempre y cuando ambos estén en la misma dirección y no deban ser sobrepasados más de una vez). Si bien se podría pensar que la reserva natural se puede definir como un factor ambiental, esto es incorrecto debido a que el centro de acopio tiene la capacidad de funcionar de manera sostenible, descartando este aspecto como el causante de la inviabilidad. Para este caso, es determinante el factor social ya que la construcción del centro de acopio alteraría las actividades de los indígenas de la zona; por encontrarse sobre una ubicación ocupada, se considera inminente su necesidad de cambio.

Al ser analizadas las coordenadas obtenidas (13; 4,17) se tiene una ubicación disponible, lo más cerca posible de la ideal. En este caso se da, al igual que en el anterior caso, una situación favorable, dado que la ubicación del emplazamiento productivo no afectará la situación del asentamiento indígena ni tampoco se ubicará en el área de la reserva natural, lo cual es favorable para el desarrollo de cualquier actividad productiva (Figura 4).

Figura 4.
Nueva ubicación del centro de distribución.

Fuente: elaboración propia

En ambos casos de aplicación del método MMRC, se evidencia lo oportuno y practico de esta herramienta matemática, dado que facilita la ubicación de emplazamientos productivos sin la afectación social, ambiental, política y/o económica que pudiera darse por la ejecución de cualquier otro método. Otro aspecto de gran relevancia con relación a la aplicación del método MMRC es la facilidad de entendimiento de este por cualquier actor productivo; además de lo sencillo, practico y económico que resulta su ejecución.

DISCUSIÓN

De acuerdo a los resultados obtenidos, se puede argumentar que la iniciativa de este nuevo Método Matemático de Recálculo de Coordenadas, denominado MMRC, es congruente con lo expuesto por autores como Feldmann y Olhager, 2013) quienes manifestaron la necesidad de ampliar la realización de evaluaciones de emplazamientos productivos con el empleo de cocientes de localización; atendiendo aspectos como ubicación geográfica y desempeño productivo; lo cual incluye el presente modelo, pero este además, adiciona aspectos de carácter intangibles (políticos, sociales y ambientales), que no están contemplados en estos métodos iniciales, y que ya se vienen argumentando en la normativa colombiana, respecto a usos del suelo en el marco de la constitución política de Colombia y la ley 388 de 1997 para la planeación y ordenamiento del territorio, entre otros. 

Es en este mismo ámbito que autores como Sánchez (2007), González (2014) y Causado, et al (2015) sostienen que existen unos condicionantes que facilitan la determinación de instalar un emplazamiento productivo de acuerdo a la concentración territorial de poder político, poder económico y los mercados internacionales. Esto es propuesto por los autores de este modelo, cuantificando estos determinantes, pero, además, reubicándolos técnicamente, en casos de solapamiento por funciones ambientales, sociales, de mercado y políticas.

CONCLUSIÓN

La toma de decisiones relevantes y de carácter estratégico, como la localización de emplazamientos productivos, ha tomado gran importancia dadas las implicaciones de carácter económico y de sostenibilidad en el establecimiento de iniciativas productivas; en este ámbito, el desarrollo del Método de Recálculo de Coordenadas – MMRC, resulta de gran importancia porque la definición de sitios ideales para el establecimiento de emplazamientos productivos, sin ningún tipo de conflictos, facilita el acopio de frutas y hortalizas a los campesinos colombianos y, además, les permite centralizar y optimizar todo el proceso de acopio y comercialización de manera continua.

Mediante la aplicación del MMRC también es factible recalcular las coordenadas de ubicación de los emplazamiento productivos, sobre todo en algunos casos complejos que incluyen factores medioambientales, sociales, y políticos adicionales. Por estas razones, contar con una nueva herramienta como el MMRC aporta en la reducción de riesgos de toma de decisiones de inversión que representan un desafío al desarrollo productivo. 

Adicionalmente, se puede aseverar que mediante el método MMRC se logró el propósito de definir un nuevo proceso técnico de las condiciones que impiden la localización de una instalación en un momento determinado, a partir del recálculo de las coordenadas geográficas que permitan la definición de nuevos escenarios en los cuales se puedan implantar emplazamientos mediante la adopción de una solución óptima. Es importante tener en cuenta que la fiabilidad del análisis cuantitativo es directamente proporcional a la calidad de la fase cualitativa previa y que se debe definir el escenario macro de la situación para definir correctamente las direcciones de movimiento de coordenadas. Cada caso estudiado merece un análisis propio, dado que presenta condiciones singulares que determinan la postura del o de los expertos a cargo del análisis.

Finalmente, se requiere seguir profundizando en la aplicación de esta herramienta, en nuevos escenarios y en nuevos ámbitos productivos, tal como el ordenamiento territorial, y en combinación con nuevas herramientas técnicas de la ingeniería industrial, tal como la simulación de escenarios dinámicos, la programación lineal y, por último, mayor profundización en la mejor definición de los criterios de valoración y/o jerarquización de los factores inmersos en las ecuaciones que conforman el método de interés.

Concerning future research, and seeking to continue the studies on innovation non-R&D, it would be important to investigate the mechanisms that would generate higher levels of efficiency between the articulation of productivity policies and the promotion of innovation of the organizations through non-R&D capabilities. This would allow shaping to a non-traditional theory of innovation, in which, not only are organizations taken into account as spaces in which innovation is directly incorporated but also, great value would be assigned to public policies, as catalysts of innovation promoted from the state level.